ペントミノの解を求めるプログラム高速化
前回までにペントミノの解をすべて、求められるようになった。実行してみると、完了するまでに20分くらいかかる。当初に比べればこれでもかなり高速化したのだけど、まだまだ高速化の余地はありそう。チャレンジしてみる。
- 最初は、6行10列のボードに敷き詰めようとして、3時間15分経過しても800解しか出力できなかった。
- つぎに、ボードの縦横を入れ替えて10行6列にし、50分で9356解を出力した。
- 現状は、重複解を排除するように変更し、20分で2339解を出力する。
$ time python pentomino.py
...中略...
解合計 2339
操作数 10385817
real 18m56.501s
user 18m47.271s
sys 0m1.475s
現状のコード
# coding: utf-8 import numpy as np # すべてピース形状をPieceオブジェクトの配列に保存する class Piece: def __init__(self, s, h,m,n): a = np.array(map(int, s)).reshape(h, -1) self.used = False self.form = [] for i in range(m): for j in range(n): self.form.append((a, a.argmax())) a = np.rot90(a) a = np.fliplr(a) pp = [Piece('010111010', 3,1,1), Piece('111101', 2,1,4), Piece('110011001', 3,1,4), Piece('110011010', 3,1,2), Piece('110010011', 3,2,2), Piece('111110', 2,2,4), Piece('11100011', 2,2,4), Piece('11110100', 2,2,4), Piece('111010010', 3,1,4), Piece('11111000', 2,2,4), Piece('111100100', 3,1,4), Piece('11111', 1,1,2)] # パズルの解を求める def try_piece(board, pp, x, y, lvl): global counter global try_counter try_counter += 1 board_h, board_w = board.shape for i, piece in enumerate(pp): if not piece.used: for form in piece.form: piece_matrix, piece_origin = form h, w = piece_matrix.shape ox = x - piece_origin # ピースが飛び出したらそこから先は見ない if ox < 0 or ox + w > board_w or y + h > board_h: continue board_section = board[y:y + h, ox:ox + w] # ピースがかぶったらそこから先は見ない if (board_section * piece_matrix).any(): continue # ピースを置く board_section += piece_matrix * (i + 1) pp[i].used = True # すべてのピースを置ききったらTrueを返す(recursiveコールの終了) if lvl == 11: counter += 1 print 'No', counter print np.rot90(board) print # ピースを戻す board_section -= piece_matrix * (i + 1) pp[i].used = False return True # 次のピースを試す k = board.argmin() try_piece(board, pp, k % board_w, k // board_w, lvl + 1) # ピースを戻す board_section -= piece_matrix * (i + 1) pp[i].used = False return False counter = 0 try_counter = 0 board = np.zeros((10, 6)) try_piece(board, pp, 0, 0, 0) print '解合計', counter print '操作数', try_counter
1次元配列化
- 2次元配列を扱うnumpyは素晴らしい使い心地なのだけど、たぶん処理の負荷は高いのだと思う。
- 各ピースはすべて5つの正方形の組み合わせで構成されている。
- ところがピースの形状データは、最大3×3=9つの要素を持つ2次元配列で表現している。
- ブロック数の倍近い要素数で、行列演算で重なり判定や置き換えを常に処理することになる。
- また、2次元配列といってもメモリ中では常に1次元の状態で保存されているはず。
- 単にコードが2次元配列的な表現になっているだけで、内部ではnumpyが1次元配列に変換して処理しているのだと思う。
- numpyは人間の思考に楽をさせてくれるけど、それに甘えていると高速化できない。
- 高速化を求めるならnumpyを使わずに、自分の思考をフル回転させる必要がある。
board配列の1次元化
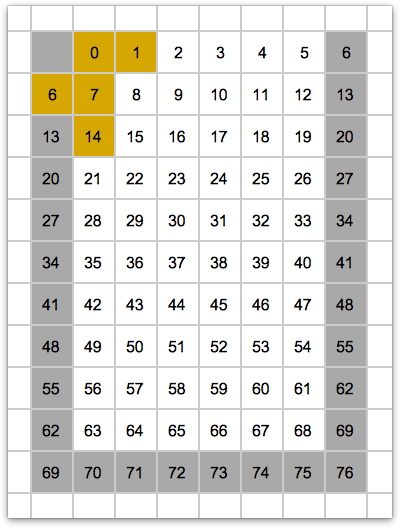
- まず、11行×7列の以下のような配列をイメージする。
- イメージとしては2次元で書いているけど、配列は1次元である。
- 各マスの数字は、1次元配列のインデックスである。
- グレーの部分は、行の末尾と列の末尾を区別するために追加している。
- 例えばインデックス6は、1行ずれて両サイドに表現しているが、
- 実際の1次元配列内部が以下のように連続したものであるため。
-
- インデックス5の次はインデックス6であり、インデックス7の手前はインデックス6なのである。
- それを2次元的に補うため、両サイドに表現しているのだ。
- 1次元配列で2次元的な空間を表現する工夫である。
- board配列は0で初期化するのだけど、グレー要素には100を設定しておく。
- board配列はいずれpiece番号で埋まっていくので、piece番号と区別できる必要がある。
- 100に限らずpiece番号より大きい数値であれば、何でもいい。
>>> board = np.zeros(11 * 7)
>>> for i, b in enumerate(board):
... if (i + 1) % 7 == 0 or i >= 70: board[i] = 100
...
>>> board
array([ 0., 0., 0., 0., 0., 0., 100., 0., 0.,
0., 0., 0., 0., 100., 0., 0., 0., 0.,
0., 0., 100., 0., 0., 0., 0., 0., 0.,
100., 0., 0., 0., 0., 0., 0., 100., 0.,
0., 0., 0., 0., 0., 100., 0., 0., 0.,
0., 0., 0., 100., 0., 0., 0., 0., 0.,
0., 100., 0., 0., 0., 0., 0., 0., 100.,
0., 0., 0., 0., 0., 0., 100., 100., 100.,
100., 100., 100., 100., 100.])
piece形状の1次元化
- 各ピース形状の左上のブロックをインデックス0に合わせて置いてみる。
- 例えばFピースなら、以下のようになる。
- [0, 1, 6, 7, 14]という座標は、board配列内でFピースを描くための情報となる。
- 上記座標を覚えておけば、board配列の任意の位置にFピースを復元できるのだ!
- すべてのピースを左上原点に合わせて、1次元座標を求めておく。
>>> # coding: utf-8
... import numpy as np
>>>
>>> # すべてのピース形状をPieceオブジェクトの配列に保存する
... class Piece:
... def __init__(self, s, h,m,n):
... a = np.array(map(int, s)).reshape(h, -1)
... self.used = False
... self.form = []
... for i in range(m):
... for j in range(n):
... self.form.append((a, a.argmax()))
... a = np.rot90(a)
... a = np.fliplr(a)
...
>>> pp = [Piece('010111010', 3,1,1),
... Piece('111101', 2,1,4),
... Piece('110011001', 3,1,4),
... Piece('110011010', 3,1,2),
... Piece('110010011', 3,2,2),
... Piece('111110', 2,2,4),
... Piece('11100011', 2,2,4),
... Piece('11110100', 2,2,4),
... Piece('111010010', 3,1,4),
... Piece('11111000', 2,2,4),
... Piece('111100100', 3,1,4),
... Piece('11111', 1,1,2)]
>>>
>>> for i, piece in enumerate(pp):
... piece.loc_form = []
... for form in piece.form:
... a = []
... for r, row in enumerate(form[0]):
... for c, col in enumerate(row):
... if col: a.append(r * 7 + c - form[1])
... piece.loc_form.append(a)
...
>>> pp[0].loc_form
[[0, 6, 7, 8, 14]]
>>> pp[1].loc_form
[[0, 1, 2, 7, 9], [0, 1, 7, 14, 15], [0, 2, 7, 8, 9], [0, 1, 8, 14, 15]]
1次元配列を利用して解を求める
- 以上の1次元配列を使ってパズルの解を求めるコードに修正してみた。
- numpyを利用するのは解を出力する時だけとなった。
- ピースが置けるかどうかの判定やピースを置く・戻す処理は、単純な変数同士の演算で処理している。
- try_peiceの呼び出し回数は、1000万回を超えている!
- try_pieceの書き方が高速化に大きな影響を及ぼすはず。
# パズルの解を求める
-def try_piece(board, pp, x, y, lvl):
+def try_piece(board, pp, lvl):
global counter
global try_counter
try_counter += 1
- board_h, board_w = board.shape
+ x = board.argmin()
for i, piece in enumerate(pp):
if not piece.used:
- for form in piece.form:
- piece_matrix, piece_origin = form
- h, w = piece_matrix.shape
- ox = x - piece_origin
- # ピースが飛び出したらそこから先は見ない
- if ox < 0 or ox + w > board_w or y + h > board_h: continue
- board_section = board[y:y + h, ox:ox + w]
- # ピースがかぶったらそこから先は見ない
- if (board_section * piece_matrix).any(): continue
+ for blocks in piece.loc_form:
+ if board[x + blocks[0]] or board[x + blocks[1]] or board[x + blocks[2]] or board[x + blocks[3]] or board[x + blocks[4]]: continue
# ピースを置く
- board_section += piece_matrix * (i + 1)
- pp[i].used = True
+ for b in blocks: board[x + b] = i + 1
+ piece.used = True
# すべてのピースを置ききったらTrueを返す(recursiveコールの終了)
if lvl == 11:
counter += 1
print 'No', counter
- print np.rot90(board)
+ print np.rot90(board.reshape((11, -1))[0:10, 0:6])
# ピースを戻す
- board_section -= piece_matrix * (i + 1)
- pp[i].used = False
+ for b in blocks: board[x + b] = 0
+ piece.used = False
return True
# 次のピースを試す
- k = board.argmin()
- try_piece(board, pp, k % board_w, k // board_w, lvl + 1)
+ try_piece(board, pp, lvl + 1)
# ピースを戻す
- board_section -= piece_matrix * (i + 1)
- pp[i].used = False
+ for b in blocks: board[x + b] = 0
+ piece.used = False
return False
counter = 0
try_counter = 0
-board = np.zeros((10, 6))
-try_piece(board, pp, 0, 0, 0)
+try_piece(board, pp, 0)
print '解合計', counter
print '操作数', try_counter
修正後のコード
- boardサイズを可変できるように変数browとbcolで一般化して、以下のようなコードが完成。
# coding: utf-8 import numpy as np # 参照だけならメソッド定義内でも常にグローバルスコープ # 書き込みする場合はメソッド定義内でglobal宣言が必要 brow, bcol = 10, 6 # すべてのピース形状をPieceオブジェクトの配列に保存する class Piece: def __init__(self, s, h,m,n): a = np.array(map(int, s)).reshape(h, -1) self.used = False self.form = [] for i in range(m): for j in range(n): self.form.append((a, a.argmax())) a = np.rot90(a) a = np.fliplr(a) pp = [Piece('010111010', 3,1,1), Piece('111101', 2,1,4), Piece('110011001', 3,1,4), Piece('110011010', 3,1,2), Piece('110010011', 3,2,2), Piece('111110', 2,2,4), Piece('11100011', 2,2,4), Piece('11110100', 2,2,4), Piece('111010010', 3,1,4), Piece('11111000', 2,2,4), Piece('111100100', 3,1,4), Piece('11111', 1,1,2)] for i, piece in enumerate(pp): piece.loc_form = [] for form in piece.form: a = [] for r, row in enumerate(form[0]): for c, col in enumerate(row): if col: a.append(r * (bcol + 1) + c - form[1]) piece.loc_form.append(a) # boardの初期化 board = np.zeros((brow + 1) * (bcol + 1)) for i, b in enumerate(board): if ((i + 1) % (bcol + 1)) == 0 or i >= ((bcol + 1) * brow): board[i] = 100 # パズルの解を求める def try_piece(board, pp, lvl): global counter, try_counter try_counter += 1 x = board.argmin() for i, piece in enumerate(pp): if not piece.used: for blocks in piece.loc_form: if board[x + blocks[0]] or board[x + blocks[1]] or board[x + blocks[2]] or board[x + blocks[3]] or board[x + blocks[4]]: continue # ピースを置く for b in blocks: board[x + b] = i + 1 piece.used = True # すべてのピースを置ききったらTrueを返す(recursiveコールの終了) if lvl == 11: counter += 1 print 'No', counter print np.rot90(board.reshape((brow + 1, -1))[0:brow, 0:bcol]) print # ピースを戻す for b in blocks: board[x + b] = 0 piece.used = False return True # 次のピースを試す try_piece(board, pp, lvl + 1) # ピースを戻す for b in blocks: board[x + b] = 0 piece.used = False return False counter = 0 try_counter = 0 try_piece(board, pp, 0) print '解合計', counter print '操作数', try_counter
実行すると...
$ time python pentomino.py
解合計 2339
操作数 10385817
real 2m58.318s
user 2m56.990s
sys 0m0.304s
3分切った!
参考ページ
以下のページがたいへん参考になりました!感謝です!
- Pythonの数値計算ライブラリ NumPy入門 « Rest Term
- 素敵なnumpyの使い方がとってもよく分かった。