天地明察で円の直径はどのように求められたのか？

雑記

いいかげん遅過ぎたが、天地明察を読んだ。

読み始めて暫くすると、その世界に深く引きずり込まれた。*1その中で、最初の方で出題された図形問題がある。

      • 第一章　一瞥即解　一の中盤（P21）

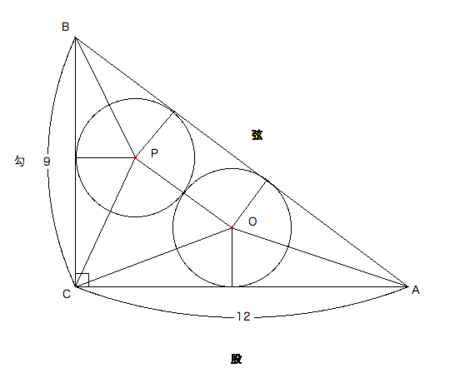
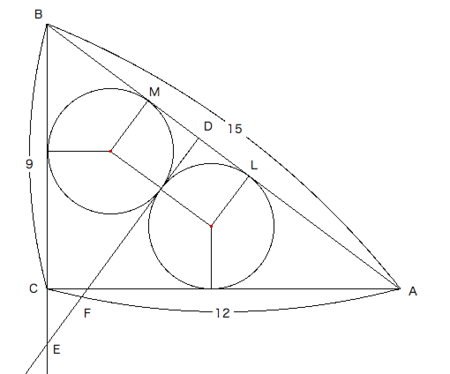
今、釣（つり＝高さ）が9寸、股（こ＝底辺）が12寸の勾股弦（こうこげん＝直角三角形）がある。その内部に、図のごとく、直径が等しい円を二つ入れる。円の直径を問う。

  • 円は三角形に内接し、互いに外接していると解釈した。

この問題を関孝和は一瞬で回答する。渋川春海は数日考えてようやく答えに辿り着く。自分は、30分考えたが先が見えず、そのまま小説の世界に引きずり込まれてしまう。結局読み終わった今でも、答えは分かっていてもそこに至る考え方を理解していない。小説を読んでいる最中から気になって仕方なかったことなので、読み終わった今、徹底的に考えてみることにした。

      • これから天地明察を読む方へ：この図形問題の回答が先に分かったとしても、天地明察の話しの主流は別の所にあるので、小説は変わらず面白く読めると考えています。但し、これはあくまでも自分の感想なので、全く何も知らない無の状態で読み始めたい、という方もいるかもしれません。以下に、自分なりのこの問題の解き方を書きますので、ご注意ください。

自己流の解き方

  • まず、問題の図に以下のように補助線を入れた。

  • 三角形ABCは三平方の定理より斜辺AB=15。
  • 斜辺ABを底辺とした時の三角形ABCの高さhは、
15×h/2 = 12×9/2
15h = 108
h = 108/15 = 36/5
  • ところで、円の中心から接線の接点に引いた直線は垂直になるので、
  • 三角形ACO、三角形BCP、台形ABPO、三角形OPCの面積は、円の半径をrとして以下のように表現できる。
    • 三角形ACO=12r/2
    • 三角形BCP=9r/2
    • 台形ABPO=(2r+15)×r/2
    • 三角形OPC=2r×(36/5-r)/2
      • 辺OPと辺ABは平行なので、三角形OPCの高さは、三角形ABCの高さ36/5から、円の半径rを引いた値になるのだ。（これに気付くのに時間がかかった）
  • 以上の三角形と台形の面積を足し算すれば、12×9/2と等しくなるはずである。
12r+9r+(2r+15)r+2r(36/5-r)=12×9 ...... 両辺を2倍して"/2"は削除した
12r+9r+2r^2+15r+(72/5)r-2r^2=108
36r+(72/5)r=108
180r+72r=540 ...... 両辺を5倍した
252r=540
r=540/252 = 90/42 = 15/7 ...... 6で2回約分した
  • 問題は円の直径を問うので2倍して、答え30/7。

なんとか解けたが、その過程では非常に煩雑な数式の計算が必要である。果たして、関孝和はこのような計算を瞬時にできたのだろうか？

渋川春海の解き方

渋川春海は、小説の中で以下のように回答している。

      • 第二章　算法勝負　二の終盤（P97）

術曰く。まず勾股を相乗し、これを二段（2倍）。さらに勾股弦の総和にて除（割る）。これに弦を乗（掛ける）し、また勾股の和にて除なり。

  • まず勾股を相乗し、これを二段（2倍）。
    • 9×12×2＝216
  • さらに勾股弦の総和にて除（割る）。
    • 216÷(9+12+15)= 216/36 = 6
  • これに弦を乗（掛ける）し、
    • 6×15＝90
  • また勾股の和にて除なり。
    • 90÷(9+12)=90/21=30/7

30/7が導かれるが、この数式は一体何をしているのか？答えは分かったが、数式の意味がずっと分からなかった。気になって仕方がなかった。でも小説の世界に引き込まれて、話しの続きも立ち止まらずに読みたくて、分からないまま今に至る。

直角三角形に内接する円の性質

この数式を理解するには、三角形の内接円の半径rを求める公式を理解しておく必要がある。

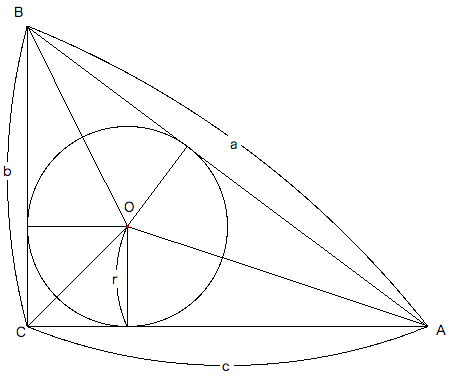
  • 直角三角形に内接する円の半径rは以下の数式で求められる。
bc/(a+b+c)
  • なぜなら、三角形ACO・三角形BCO・三角形ABOの面積の和と、三角形ABCの面積が等しいことを数式にしてみると、
(cr+br+ar)/2 = bc/2
cr+br+ar = bc
r(a+b+c) = bc
r = bc/(a+b+c)
  • r = bc/(a+b+c) が導き出された！
相似な三角形を見つける
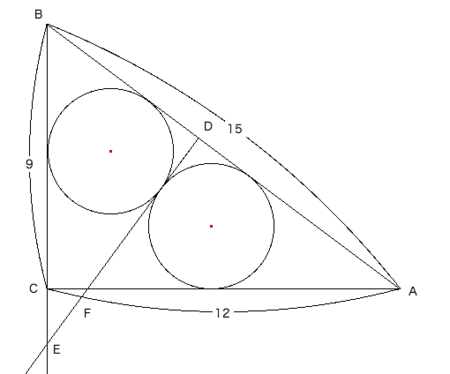
  • 次に、二つの内接円の接点に一本の接線を引くことで、見えてくる三角形がある。

  • 三角形ABCと三角形AFDと三角形EBDは、相似である。
    • なぜなら、三角形ABCと三角形AFDは、角Aを共有した直角三角形のため、３角が同じ*2角度となる。
    • 同様に、三角形ABCと三角形EBDは、角Bを共有した直角三角形のため、３角が同じ角度となる。
    • つまり、3つの三角形は相似である。
  • さらに、三角形AFDと三角形EBDは、合同になる。
    • なぜなら、同じ半径の内接円を持ち、かつ相似な三角形なので、合同なのだ。
相似比を利用する
  • まず、上記で理解した「直角三角形に内接する円の性質」を利用して、
  • 三角形ABCに内接する円の直径を求める。それが以下の部分。
    • まず勾股を相乗し、これを二段（2倍）。......直径を求めるので、ここで2倍しているのだ。
      • 9×12×2＝216
    • さらに勾股弦の総和にて除（割る）。
      • 216÷(9+12+15) = 216/36 = 6
  • そして、三角形AFDに内接する円の直径を、以下の相似比を利用して求めている。
    • 辺AD+辺DF：辺AC+辺CB
    • 三角形AFDと三角形EBDは合同なので、辺DFは辺BDと等しい。
    • よって、辺AD+辺DF＝15。
    • 辺AC+辺CB＝9+12＝21なのは、設問から明白。
  • 三角形AFDの内接円の直径を求めるために、上記の15：21を利用しているのが以下の部分。
    • これに弦を乗（掛ける）し、
      • 6×15＝90
    • また勾股の和にて除なり。
      • 90÷(9+12)=90/21=30/7
  • つまり、三角形ABCに内接する円の直径6に、相似比15/21を掛けていたのだ。

6×15/21 = 30/7。明察！

関孝和の解き方

関孝和は答え30/7しか記していないので、以下は自分の想像である。果たして、渋川春海の数式を瞬時に暗算していたのだろうか？暗算に長けていれば、可能だろう。しかし、関孝和は小説の中で一瞥即解。問題をチラ見して、何の迷いもなく答えのみ書いている。おそらく、さらにエレガントな手順があるに違いない。そう考えるのが自然。

3:4:5の直角三角形に内接する円の性質

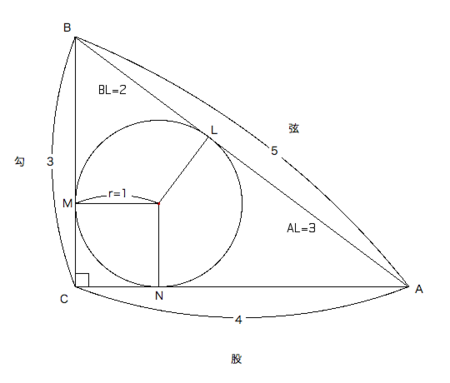
  • 3:4:5の直角三角形に内接する円では、半径と各辺の長さが上記のような比となる。
  • 内接円の半径をrとすると、
  • 辺CM=rなので、辺BM=3-r。
  • 辺BM＝辺BLなので、辺BL＝3-r。
  • 同様に辺CN＝rなので、辺AN=4-r。
  • 辺AN=辺ALなので、辺AL=4-r。
  • 辺AB＝辺BL+辺AL、に代入してみた。
5=3-r+4-r
5=-2r+7
2r=2
r=1
  • つまり、半径r=1となり、
    • 辺CM:辺BM=1:2
    • 辺CN:辺AN=1:3
    • 辺BL:辺AL=2:3
  • 以上のような綺麗な比となるのだ！
二つの合同な三角形から比で求める
  • ここで、渋川春海が見つけた相似な三角形に、以下のような補助線を入れて眺めてみる。

  • すると、三角形AFDと三角形EBDは合同であり、三角形ABCと相似なので、
  • 3:4:5の直角三角形に内接する円の性質より、
    • 辺DM:辺BM＝1:2
    • 辺DL:辺AL=1:3
  • よって、辺ABは7等分すると、円の半径r=15/7となる。
  • 求められているのは円の直径なので2倍して、30/7。明察！


素晴らしくシンプルに求められた！

  • おそらく、関孝和は3:4:5の直角三角形に内接する円の性質を利用したに違いない。
  • 三角形に内接する二つの円と見せかけて、その実体は三角形に内接する一つの円の問題だと見破る能力。
  • 自分にはその能力がなくて、最も冗長な手段となってしまった...。

参考

  • GeoFlair
    • GeoFlairのダウンロード : Vector ソフトを探す！
    • 作成した図形を保存できないが、試用可能。
    • 数学の図形問題を素晴らしく正確に作図できる！
    • やってみると分かるが、これがないとこの日記に挿入した図を描くのは、めちゃくちゃ面倒である。
    • 最新のcocoa環境に対応して欲しいなあ。

*1:実は当初、図書館で借りたのだが、返却日の2日前になってやっと読み始めた。当然読み切れるはずもなく、しかし、小説の世界に引き込まれたまま終われず、即購入して続きを読みふけったのであった。満足した。

*2:1角を共有する直角三角形なので、2角が等しい。よって、残りの1角も等しい。